一般线性规划问题中当线性方程组的变数数大于方程个数,这时会有不定数量的解,而单纯形法是求解线性规划问题的通用方法。
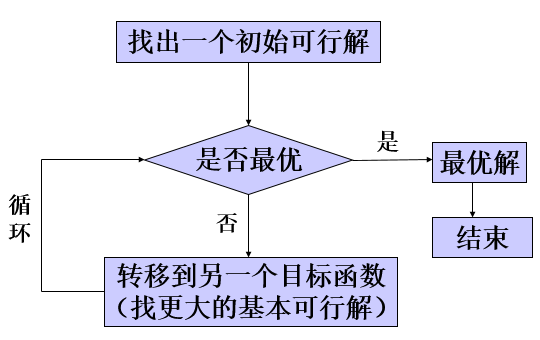
具体步骤是,从线性方程组找出一个个的单纯形,每一个单纯形可以求得一组解,然后再判断该解使目标函式值是增大还是变小了,决定下一步选择的单纯形。通过最佳化叠代,直到目标函式实现最大或最小值。
换而言之,单纯形法就是秉承“保证每一次叠代比前一次更优”的基本思想:先找出一个基本可行解,对它进行鉴别,看是否是最优解;若不是,则按照一定法则转换到另一改进后更优的基本可行解,再鉴别;若仍不是,则再转换,按此重複进行。因基本可行解的个数有限,故经有限次转换必能得出问题的最优解。如果问题无最优解,也可用此法判别。
基本介绍
- 中文名:单纯形法
- 外文名:Simplex algorithm
- 提出者:G.B.丹齐克(George Bernard Dantzig)
- 提出时间:1947年
- 套用学科:数学
- 适用领域範围:运筹学线性规划
- 适用领域範围:数学 统计学
发展简史
原单纯形法
线性规划问题是研究线上性约束条件下,求线性函式的极值问题。线性规划是运筹学的一个重要分支, 也是最早形成的一个分支。线性规划的最优性条件,又称为Karush-Kuhn-Tucker(KKT)条件。不等式约束问题的必要和充分条件初见于卡罗需(William Karush)的博士论文,之后在一份由W.库恩(Harold W. Kuhn)及塔克(Albert W. Tucker)撰写的研讨生论文出现后受到重视。
线性规划的集大成者是G.B.丹齐克(George Bernard Dantzig)。1947 年,面对美国制定空军军事规划时提出的问题,丹齐克首次提出了单纯形法来解决这类极值问题的求解。单纯形法是年由创建的对所有一般线性规划问题的最早的可行算法。1953年,他又提出了改进单纯形法。
但原单纯形法不是很经济的算法。许多数学家在随后提出更有效率的算法,如改进单纯形法、对偶单纯形法等。
改进单纯形法
1953年美国数学家G.B.丹齐克为了改进单纯形法每次叠代中积累起来的进位误差,提出改进单纯形法。其基本步骤和单纯形法大致相同,主要区别是在逐次叠代中不再以高斯消去法为基础,而是由旧基阵的逆去直接计算新基阵的逆,再由此确定检验数。这样做可以减少叠代中的累积误差,提高计算精度,同时也减少了在计算机上的存储量。
对偶单纯形法
1954年美国数学家C.莱姆基提出对偶单纯形法(Dual Simplex Method)。单纯形法是从原始问题的一个可行解通过叠代转到另一个可行解,直到检验数满足最优性条件为止。对偶单纯形法则是从满足对偶可行性条件出发通过叠代逐步搜寻原始问题的最优解。在叠代过程中始终保持基解的对偶可行性,而使不可行性逐步消失。设原始问题为min{cx|Ax=b,x≥0},则其对偶问题(Dual Problem)为 max{yb|yA≤c}。当原始问题的一个基解满足最优性条件时,其检验数cBB^(-1)A-c≤0。即知y=cBB^(-1)(称为单纯形运算元)为对偶问题的可行解。所谓满足对偶可行性,即指其检验数满足最优性条件。因此在保持对偶可行性的前提下,一当基解成为可行解时,便也就是最优解。
下山单纯形法
数学最佳化中,由George Dantzig发明的单纯形法是线性规划问题的数值求解的流行技术。有一个算法与此无关,但名称类似,它是Nelder-Mead法或称下山单纯形法,由Nelder和Mead发现(1965年),这是用于最佳化多维无约束问题的一种数值方法,属于更一般的搜寻算法的类别。
这二者都使用了单纯形的概念,它是N维中的N+1个顶点的凸包,是一个多胞体:直线上的一个线段,平面上的一个三角形,三维空间中的一个四面体,等等。
定理定义
标準形式
由于目标函式和约束条件内容和形式上的差别,线性规划问题可以有多种表达式。因此,为了便于讨论和制定统一的算法,在制定单纯形法时,规定使用单纯形法求解的线性规划问题需要有一个标準形式,它有下面三个特徵:
(1) 标準形式目标函式统一为求极大值或极小值,但单纯形法主要用来求解极大值;
(2) 所有约束条件(除非负条件外)都是等式,约束条件右端常数项bi全为非负值;
(3) 所有变数的取值全为非负值。
下式为满足上述特徵的线性规划问题的标準形式:
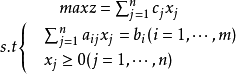
其中,目标函式中的变数xj(x1,x2,…xn)称为决策变数(控制变数),它的取值受m项资源的限制,它的係数称为价值係数cj。s.t.括弧下的内容是约束条件,用bi(i=1,···,m)表示第i种资源的拥有量,用aij表示变数xj取值为1个单位时所消耗或含有的第i种资源的数量,通常称aij为技术係数或工艺係数。
除非负条件外的n个约束条件所组成的n元方程组,若可解可求出n个变数xj的值。求出的n个变数所构成的列向量X=(x1,···xn)T,若能再满足非负条件(即决策变数满足所有约束条件),称为线性规则问题的可行解。使得目标函式值z达到max最大的可行解即为最优解,求解线性规划问题的目的就是要找出目标函式的最优解。
下图为上式标準形式的线性规划问题的展开型:

但是线性规划问题往往并非标準形式的,如下图所示。

因此,在用单纯形法求解前,需要将目标函式转化为标準形式。这个过程包括四个个部分的转换:
(1) 目标函式的转换:统一求极大值,若是求极小值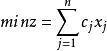 ,则可将目标函式乘以(-1),即化为
,则可将目标函式乘以(-1),即化为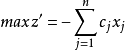 。
。
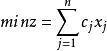
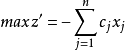
(2)变数的转换:对于已经是大于等于零的变数xj≥0不做变化。
对于小于等于零的变数xj,取负号令其变为大于等于的变数xj',若xj≤0,则xj'=-xj,xj'≥0;
若xj取值无约束,可令新的两个非负变数xj'和xj''相减,即xj=xj'-xj'',其中xj',xj''≥0。
(3)约束条件的右端项常数的转换:bi<0时,只需将等式或不等式两端同乘(-1),则
(4) 约束条件的转换:将所有不等式全部转换为等式。
为此,对于“≤ ”型约束加入一个变数xs,对于“≥ ”型约束则减去一个变数xs。加到原约束条件中的变数,称为剩余变数或鬆弛变数,在实际问题中它表示未被充分利用的资源和超出资源数。由于此部分资源均未转化为价值和利润,所以在引进模型后这些变数在目标函式中的係数均为零。
此外,为了构造出初始基变数,对于“ = ”型约束和“≥ ”型约束还需要加上人工变数。人工变数构成天然的初始基变数,其係数为1和其它行的人工变数的係数为0(故因此一般省略,不写出)的特殊构造,组成最简单的线性无关矩阵——单位矩阵。对于原约束条件中若已有线性无关的基向量,可以不需要再加入人工变数。但为避免出错和算法的统一性,一般情况下面对“ = ”型约束和“≥ ”型约束不应省略人工变数。
按照以上的转规则,将上述的列线性规划问题化为标準形式,其结果如下:

矩阵形式
为了运算简洁,单纯性法的表示与定理的说明往往用矩阵形式说明。上述的标準形式的单纯形法用矩形形式表示如下:
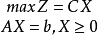
其中,C=(c1,c2,cm)为行向量,X=(x1,x2,xm)T,b=(b1,···,bm)≥0均为列向量;
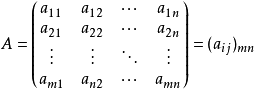
且只讨论m<n的情形,因为方程数量比变数数目多,必定有唯一解,不需要单纯形法来计算最优解。
向量形式
如果向量形式表示係数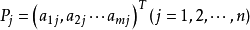 ,那幺即可将矩阵A分块,A=(P1,P2,···,Pn)。可用向量将约束条件
,那幺即可将矩阵A分块,A=(P1,P2,···,Pn)。可用向量将约束条件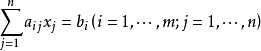 改写为
改写为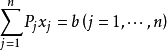 。
。
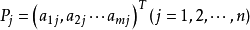
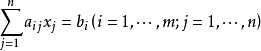
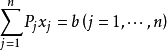
故标準形式的单纯形法用向量形式表示如下:
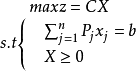
约束方程组的係数矩阵A的任意一个m ×m阶的非奇异(满秩)子方阵B,其列向量线性无关,即方程中任一向量可由这些向量线性表出,故称为线性规划的一个基矩阵,简称为基。基矩阵B中的每一个列向量Pj=(j=1,...,m)称为基向量,与基向量Pj对应的变数xj称为基变数。不失一般性,可假设:
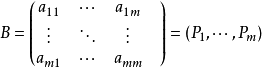
除基变数以外的变数Pi=(i=m+1,...,n)称为非基变数。并记非基矩阵为:
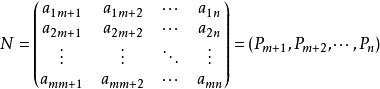
係数矩阵A可以写成分块形式A=(B,N),将基变数的向量记为Xb=(x1,x2,···,xm)T,
非基变数组成的向量记为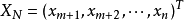 ,向量X也可以写成分块形式
,向量X也可以写成分块形式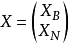
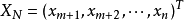
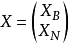
将此A和X的分块形式带入到约束方程组AX=b,得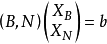 。由矩阵的乘法得
。由矩阵的乘法得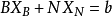 。又因为B是非奇异矩阵,所以B-1存在,将此式两边乘以B-1,移项后得
。又因为B是非奇异矩阵,所以B-1存在,将此式两边乘以B-1,移项后得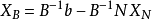 。可以把XN看作一组自由变数(又称独立变数),给它们任意一组值
。可以把XN看作一组自由变数(又称独立变数),给它们任意一组值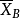 ,于是
,于是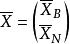 。这就是约束方程组的一个解。
。这就是约束方程组的一个解。
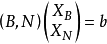
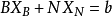
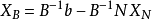
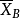
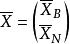
特别地,令所有的非基变数为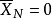 时,则
时,则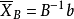 ,把约束方程组的这种特殊形式的唯一解,把约束方程组的这种特殊形式的解
,把约束方程组的这种特殊形式的唯一解,把约束方程组的这种特殊形式的解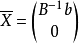 ,称为基解。或者说,因为满秩
,称为基解。或者说,因为满秩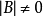 ,根据克莱姆法则或高斯消去法,由m个约束变数可解出m个基变数的唯一解。则方程组
,根据克莱姆法则或高斯消去法,由m个约束变数可解出m个基变数的唯一解。则方程组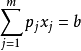 有唯一解XB=(x1,...,xm)T,将这个解加上非基变数取0的值是Ax=b的一个解:X=(x1,x2,...,xm,0,...,0)T,称X为线性规划问题的一个基解或基本解。而满足标準形式的非负约束条件x≥0的基解称为基本可行解,简称基可行解,对应于基可行解的基称为可行基。
有唯一解XB=(x1,...,xm)T,将这个解加上非基变数取0的值是Ax=b的一个解:X=(x1,x2,...,xm,0,...,0)T,称X为线性规划问题的一个基解或基本解。而满足标準形式的非负约束条件x≥0的基解称为基本可行解,简称基可行解,对应于基可行解的基称为可行基。
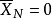
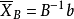
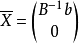
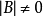
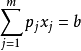
由此可见,有一个基就可以求出一个基解。基解的非零分量的个数不大于方程个数m,基B的列是从A的n列中选取线性无关的m列,其选法最多共有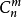 种,故基的个数或者说一个线性规划问题的基本解的总数不超过
种,故基的个数或者说一个线性规划问题的基本解的总数不超过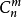 个。
个。
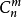
验证推导
图解法
从二维的线性规划问题的图解法简单直观,有助于了解线性规划问题的基本原理。非负条件x1、x2≥0是指坐标轴的第一象限。在以x1、x2为坐标轴的直角左边系,,每个约束条件都代表一个半平面。右图中同时满足x1+x2≤150,x1+2x2≤170,3x2≤180和x1、x2≥0的约束的点,必然落在x1、x2坐标轴和这个三个半平面教程的区域见右图的蓝色框部分,蓝色部分区域(包括边界点的每一个点)都是这个问题的可行解,因此这个区域是线性规划问题的解集合,称它为可行域。
对于此例求解得到的最优解,但对一般线性规划问题,最优解可能出现下列情况:
①有且仅有一个最优解。
②多重最优解,存在着无穷多个最优解,不存在有限最优解;当目标函式平行于非冗余的紧约束,如果目标函式只有两个变数,在坐标轴中目标函式一定平行于某一个约束条件。在实践中,可选择最优解是有用的,可从众多解中做出选择而不会损害最优值。如模型描述的是产品利润问题,生产两种产品比生产一种产品在市场竞争中更占有多样性的优势。
③无解或无可行解,其原因在模型的约束条件之间存在着矛盾,模型的构建是不正确的。假如所有的约束都是《类型的并具有非负的右端项,则这种情况永远不会出现,因为鬆弛变数已经提供了一个可行解。对于其他类型的约束,使用人工变数,只有有一个人工变数在最优叠代中取值为正。
④无界解或无有限最优解,即没有可行解或各项约束条件不阻止目标函式的值无限增大(或向负的方向无限增大)。这是因为解空间中至少有一个解是无界的,这意味着可以无限制的增加变数的值但不破坏任何一个约束,这种情况下,解空间和最有目标值都是无界的。
⑤退化解,按最小比值θ来确定换出基的变数时,有时出现存在两个以上相同的最小比值,从而使下一个表的基可行解中出现一个或多个基变数等于零的退化解。退化解出现的原因是模型中存在多余的约束,使多个基可行解对应同一定点。当存在退化解时,就有可能出现叠代计算的循环,儘管可能性极其微小。
定理证明
从图解法可以直观地看到可行域和最优解的几何意义:所有可行解构成的集合是凸集,也可能为无界域;它们有有限个顶点,线性规划问题的每个基可行解对应可行域的一个顶点;若线性规划问有最优解,必在某顶点上得到。这个结论是通过凸集的定义和三个定理的证明所得出的,下面是详细的证明过程。
凸集及其顶点
1.凸集
凸集的概念为,集合K中任意两个点,其连线上的所有点都是集合K中的点,称集合K是凸集。虽然对简单的集合形体可以直观地判断其凹凸性,但在高维空间,只能给出点集的解析表达式,因此只能用数学解析式判断。设K是n维欧式空间的一点集,若任意两点X1∈K,X2∈K,其连线可表示为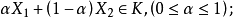 则称K为凸集。
则称K为凸集。 凸集
凸集
 凸集
凸集2.凸组合
设X1,X2,···,Xk是欧式空间En中的k个点。若存在μ1,μ2,μk,且0≤μi≤1,i=1,2,···,k;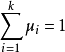 ,使X=μ1X1+μ2X2+···+μkXk,则称X为X1,X2,···,Xk的凸组合。
,使X=μ1X1+μ2X2+···+μkXk,则称X为X1,X2,···,Xk的凸组合。
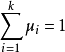
3.顶点
凸集K中满足下述条件的点X称为顶点:如果K中不存在任何两个不同的点X1,X2,使X成为这两个点连线上的一个点。或者这样叙述:对于任何X1∈K,X2∈K,不存在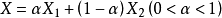 ,则称X是凸集K的顶点。
,则称X是凸集K的顶点。
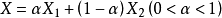
定理一
若线性规划问题存在可行解,则问题的可行域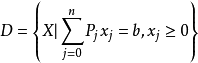 是凸集。
是凸集。
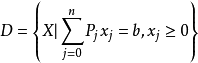
证:为了证明满足线性规划约束条件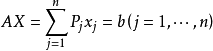 的所有点组成的几何图形D是凸集。只要证明D内任意两点X1,X2的连线上的点也必定在D内即可,下面给予证明。
的所有点组成的几何图形D是凸集。只要证明D内任意两点X1,X2的连线上的点也必定在D内即可,下面给予证明。
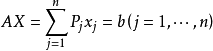
设X1=(x11,x12,...,x1n)T,X2=(x21,x22,...,x2n)T为D内任意两点,即X1∈D,X2∈D,且X1≠X2。
将X1,X2带入约束条件AX=b,则有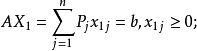
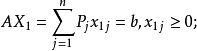
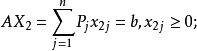
由凸集的定义,X1,X2连线上任意一点可以表示为:X=aX1+(1-a)X2(0<a<1)
两边同乘A:AX=A[aX1+(1-a)X2],将此式用向量展开式表示:
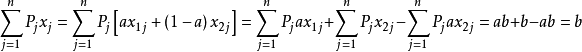
所以集合中任何两点连线上的点满足约束条件,即均在集合内,即X=aX1+(1-a)X2∈D,所以可行域是凸集。
引理一
线性规划问题的可行解X=(x1,x2,...,xn)T为基可行解的充要条件的是X的正分量所对应的係数列向量是线性独立的。
证 (1)必要性:由于基解的列向量是线性独立的,并且可行解的分量即是正分量。
(2)充分性:若向量P1,P2,···,Pk线性独立,则必定k≤m;当k=m时,它们恰构成一个基,从而X=(x1,x2,...,xk,0...0)为相应的基可行解。当k<m时,由于矩阵A的秩R(A)=m,即极大无关组的向量为m,则一定可以从其余的列向量中取出m-k个与P1,P2,···,Pk构成最大的的独立向量组(基),其对应的解恰为X,所以根据定义它是基可行解。
定理二
(极点与基可行解的等价性定理)线性规划问题基可行解X对应于线性规划问题可行域(凸集)D的顶点。
证:本定理需要证明:X是可行域顶点⇔X是基可行解,这一定理可由反证法证明。即证明:X不是可行域的顶点⇔X不是基可行解。
不失一般性,假设基可行解X的前m个分量为正。故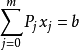 。
。
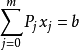
分两步来讨论,分别用反证法。
(1)若X不是基可行解,则它一定不是可行域D的顶点。
根据引理1,若X不是基可行解,则其正分量所对应的係数列向量P1,P2,···,Pm线性相关,即存在一组不全为令的数αi,i=1,2,···,m 使得α1P1+α2P2+···+αmPm=0。
用一个μ>0的数乘以上式,再分别与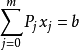 相加或相减,分别得到下列两式:
相加或相减,分别得到下列两式:
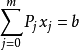
(x1-μα1)P1+(x2-μα2)P1+···+(xm-μαm)Pm=b
(x1+μα1)P1+(x2-μα2)P1+···+(xm-μαm)Pm=b
现取X1=[(x1-μα1),(x2-μα2),···,(xm-μαm),0,···0]
X2=[(x1+μα1),(x2-+μα2),···,(xm-+μαm),0,···0]
可以得出X=X1/2+X2/2,即X是X1,X2连线的中点。
另一方面,当μ充分小时,可保证xi+μαi≥0,i=1,2,···,m
即X1,X2是可行解。这证明了X不是可行域D的顶点。
(2)若X表示可行域D的顶点,则它一定不是基可行解。
因为X=(x1,x2,...,xm,0...0)不是可行域D的顶点,故在可行域D中找到不同的两点Y和Z,使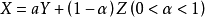 ,或可写成
,或可写成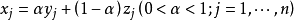 。
。
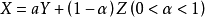
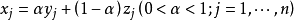
因为Y和Z是可行域的两点,应满足: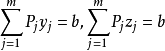
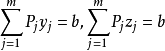
将这两式相减,即得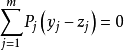
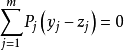
因Y≠Z,所以上式係数yi-zi不全为零,故向量组P1,P2,···,Pm线性相关,与假设矛盾。即X不是基可行解。
推论:设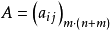 的秩为m,在非退化情况下,则X是S的顶点的充要条件是X的非0元为m个。
的秩为m,在非退化情况下,则X是S的顶点的充要条件是X的非0元为m个。
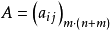
定理三
设线性规划问题有解,一定存在一个基可行解是最优解,由定理二可知必在可行域D={X|AX=b,X≥0}的某个顶点上取得最优值。这个定理分为三个部分。
定理3.1若一个问题(LP)有可行解,则它必有基可行解。
证 设X是线性规划问题的一个可行解,如果其正分量所对应的列向量P1,P2,···,Pk线性无关,由引理一可知,X是一个基可行解,定理成立。否则,需证明:从X出发,必可找到LP的一个基可行解。
因为P1,P2,···,Pk线性相关,即存在不全为零的数δ1,δ2,···,δk,使得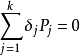 。
。
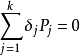
则X在可行域内必能找到两点,X1=X+εб,X2=X-εб ,其中δ=(δ1,δ2,···,δk,0,···,0)T
其中有δi≠0,取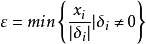 ,且必有xj±εб≥0(j=1,2,···,n) ,即X1≥0,X2≥0。
,且必有xj±εб≥0(j=1,2,···,n) ,即X1≥0,X2≥0。
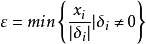
又因为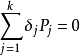 ,所以
,所以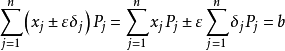 ,
,
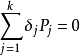
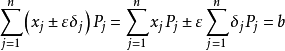
故有AX1=b,AX2=b,所以X1,X2是LP的两个可行解。
再由ε的取法可知,xj±εб≥0中,至少有一个等于零,于是所做的可行解X1和X2中,它的非零分量至少比X的减少1。如果这些非零分量所对应的列向量线性无关,则X1和X2为基可行解,定理成立。
否则,又可以X1或X2出发,重複上述步骤,再构造一个新的可行解X3或X4,使它的非零分量的个数继续减少。这样经过有限次重複之后,比可找到一个可行解Xl或X(l+1),使它的非零分量对应的列向量线性无关。因为在最坏的情况下,只有一个非零分量时,对应的只有一个非零的列向量,它必然是线性无关的,故Xl或X(l+1)必为基可行解。
定理3.2若线性规划问题有最优解,一定存在一个基可行解是最优解。
证 设X是线性规划的一个最优解,Z=CX是目标函式的最大值。若X不是基可行解,由定理二可知,X不是顶点,一定能在通过X的直线上的另外两个点,将这两个点带入目标函式有
C(X+εδ)=CX+Cεδ , C(X-εδ)=CX-Cεδ
因CX为目标函式的最大值,故有CX≥CX+Cεδ ,CX≥CX-Cεδ
Cεδ不可能为正数或负数,因此Cεδ=0,即有C(X+εδ)=CX=C(X-εδ)。
如果(X+εδ)或(X-εδ)仍不是最优解,按上面方法继续做下去,则根据定理3.1的证明方法,它的非零分量的个数比X的减少1。在最坏的情况下,只有一个非零分量时,对应的只有一个非零的列向量,它必然是线性无关的。所以一定可以找到一个基可行解,其目标函式值等于CX,问题得证。
根据定理二和定理三,可以得出如下结论:
推论一:若问题的可行域有界,则此问题的最优解一定可以在其可行域D的顶点上达到。
定理3.3设问题(LP)在多个顶点X1,X2,···,Xk出达到最优,则任意一点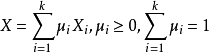 也是(LP)的最优解。
也是(LP)的最优解。
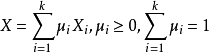
证 设目标函式的最优值为Z,则有假设有CXi=Z
由上式可知,有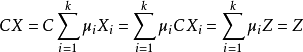
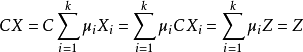
故任意一点X也是LP的最优解。X称为X1,X2,···,Xk的凸组合。
这定理说明若问题有两个或多于两个的最优解,则它就有无穷多个最优解。另外,若问题的可行域无界,则可能无有限解,也可能有有限解。若有有限解,则必可在可行域的某个顶点上达到。
叠代原理
由上述的定理3可知,如果线性问题存在最优解,一定有一个基可行解是有最优解。因此单纯形法叠代的基本思路是:先找出一个基可行解,判断其是否为最优解。如为否,则转换到相邻的基可行解,并使目标函式值不断增大,一直找到最优解为止。
初始可行基确定
对于标準型线性规划问题
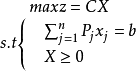
在约束条件的变数的係数矩阵总会存在一个单位矩阵作为初始可行基
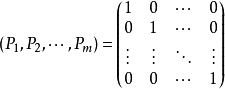
这是因为当线性规划的约束条件均为≤号,利用化为标準型的方法,在每个约束条件的左端加上一个鬆弛变数。经过整理,重新对xj和aij(i=1,2,···,m;j=1,2,···,n)进行编号,可得到以下方程组。
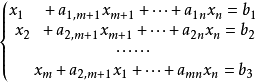
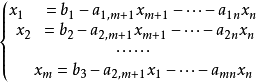
其鬆弛变数x1.···,xm的係数矩阵显然为m×m单位矩阵。 令xm+1=xm+2=···=xn=0,可得xi=bi(i=1,2,···m),又因为bi≥0,所以得到一个初始基可行解。
对约束条件为≥或=的情况,为便于初始基可行解,可以构造人工基,人为产生一个单位矩阵,可参见人工变数法。
最优性检验
对线性规划问题的求解结果可能出现唯一最优解、无穷多最优解、无界解和无可行解四种情况,为此需要建立对解的判别标準。一般情况下,经过叠代之后变成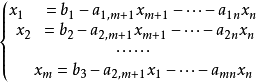
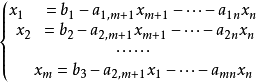
一般式为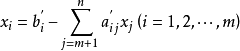
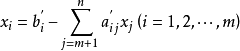
将其带入目标函式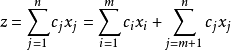 ,整理后得
,整理后得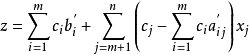
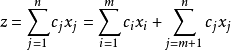
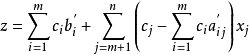
令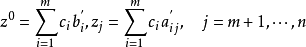 ,于是
,于是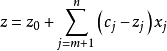
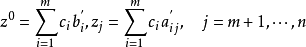
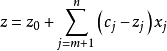
再令σj=cj-zj(j=m+1,···,n),则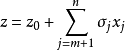
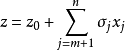
因此可以将线性规划问题的标準形式化为典式:
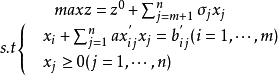
其中,称σj为检验数或判别数,它是典式的目标函式的非基变数xj(j=m+1,···,n)的係数,它又表示当某个非基变数的值改变1个单位,所引起的目标函式值的该变数,因此又称为相对价值係数。
1.最优解的判别定理
设X0=(b1',b2',···bm',0,···,0)T为对应基B的一个基可行解,且对于一切j=m+1,···,n,有σj≤0,或用向量表示σ=(0,···,0,σm+1,σm+2,···,σn)≤0,则X0为最优解。
证:设X为线性规划的任一可行解,X≥0,σ≤0,σX≤0,从而最大值z*=CX0=z0≥z0+σX=CX=z。
因为xj为正数,当σj≤0,当叠代恰好会使得z会变小(无法更优),其解即为最优。
因此σj≤0称为最优性条件,它是判别当前接是否为最优解的标準。检验数还可以写成矩阵形式σ=(σB,σN)=C-CBB-1A=(0,CN-CBB-1N)≤0,其中σB=0为基变数对应的检验数向量;σN=CN-CBB-1N为非基变数对应的检验数向量。这说明基变数的检验数必为0,并且非基变数的检验数都为负数时,才有唯一最优解。
2.无穷多最优解判别定理
若X0=(b1',b2',···bm',0,···,0)T为一个基可行解,对于一切j=m+1,···,n,又存在某个非基变数的检验数σm+k=0,则线性规划问题有无穷多最优解。
证 只需将非基变数xm+1换入基变数中,找到一个新基可行解X1。σm+k=0,z=z0,故X也是最优解。故X也是最优解。根据定理3.3可知X0和X1连线上所有点都是最优解,故有无穷多最优解。
3.基可行解的改进定理
若初始可行解X不是最优解时,需要找一个新的可行基。具体做法是从原可行解基换一个列向量(当然要保证线性独立),得到一个新的可行基,这称为基变换。为了换基,先要确定换入变数,再确定换出变数,让它们相应的係数向量进行对换,就得到一个新的基可行解。
定理内容:X0=(b1',b2',···bm',0,···,0)T对应于基B的一个基可行解,若满足下列条件:
(1)有某个非基变数xk的检验数σk>0(m+1≤k≤n);
(2)aik(i=1,2,···,m)不全小于或等于零,即至少有一个aik>0(1≤i≤m);
(3)b'i>0(i=1,2,···,m),即X0为非退化的基可行解。则从X0出发,一定能找到一个新的基可行解X1,使得CX1>CX0。
证 我们採用一种构造性的证明方法,即将X1具体地找出来,为此,我们作换基运算:
由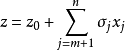 ,当某些σj>0时,增加则目标函式还可以增大,这时要将某个非基变数xj唤到基变数中去,称为换入变数。
,当某些σj>0时,增加则目标函式还可以增大,这时要将某个非基变数xj唤到基变数中去,称为换入变数。
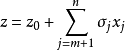
3.无界解判别定理
若X=(b1',b2',···bm',0,···,0)T为一基可行解,有一个σm+k>0,并且对i=1,2,···,m,都有a‘i,m+k≤0,那幺该线性规划问题具有无界解(或称无最优解)。
证 构造一个新的解X,它的分量为xi=b‘i-λα‘i,m+k(λ>0)
xm+k=λ
xj=0,j=m+1,···,n
因a‘i,m+k≤0,所以对任意的λ>0都是可行解,把x带入目标函式内得z=z0+λσm+k。
因σm+k>0,λ→+∞,则z→+∞,故该问题目标函式无界。
单纯形表
为检验一个基可行解是否最优,需要将其目标函式值与相邻基可行解的目标函式进行比较。为了书写规範和便于计算,对单纯形法的计算设计了一个种专门表格,称为单纯形表。叠代计算找出一个新的基可行解,就画一张单纯形表。含初始基可行解的单纯形表,称为初始单纯形表,含最优解的单纯形表,称为最终单纯形表。下图即为单纯形表的一般格式。
| Cj→ | X | ... | c1 | ... | cm | ... | cj | ... | cn |
|---|---|---|---|---|---|---|---|---|---|
CB | 基 | b | x1 | ... | xm | ... | xj | ... | xn |
c1 | x1 | b1 | 1 | ... | 0 | ... | a1j | ... | a1n |
c2 | x2 | b2 | 0 | ... | 0 | ... | a2j | ... | a2n |
... | ... | ... | ... | ... | ... | ... | |||
cm | xm | bm | 0 | ... | 1 | ... | amj | ... | amn |
cj-zj | 0 | ... | 0 | ... | 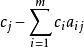 | ... | 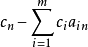 | ||
单纯形表结构为:表的第2行列出所有基变数,表的第1-3列分别列出基可行解中基变数係数、基变数和每个约束的取值(右端值)。表的第4-6列写在基变数下面是单位矩阵,非基变数xj下面数字是该变数係数向量Pj表示为基向量线性组合时的係数,即化出单位矩阵后的係数。因为P1,...,Pm是单位向量,故有:
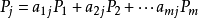
最后一行(cj-zj)写的是检验数σj。例如求第j列的检验数,只需将变数xj的係数即数字(a1j,...,amj)与CB中同行的数字(c1,...,cm)分别相乘加和,再用它上端的cj值减去乘积加和,即可得出:
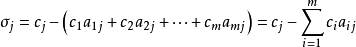
方法步骤
单纯形法的一般解题步骤可归纳如下:
①把线性规划问题的约束方程组表达成典範型方程组,典範型方程组要实现变数转换(所有变数为非负)、目标转换(统一为求极大值,若求极小值可乘以(-1))、约束转换(由不等式转化为等式)。然后,找出基本可行解作为初始基可行解。列出初始单纯形表。
②若基本可行解不存在,即约束条件有矛盾,则问题无解。
③若基本可行解存在,从初始基可行解作为起点,根据最优性条件和可行性条件,引入非基变数取代某一基变数,找出目标函式值更优的另一基本可行解。
④按步骤3进行叠代,直到对应检验数满足最优性条件(这时目标函式值不能再改善),即得到问题的最优解。
⑤若叠代过程中发现问题的目标函式值无界,则终止叠代。
图示表示如下:
 单纯形法的一般求解步骤
单纯形法的一般求解步骤用单纯形法求解线性规划问题所需的叠代次数主要取决于约束条件的个数。如今一般的线性规划问题都是套用单纯形法标準软体在计算机上求解,对于具有106个决策变数和104个约束条件的线性规划问题已能在计算机上解得。
套用例子
例1:求解下述线性规划问题,只有唯一最优解的情况。
第一步:将一般形式转换为标準形式:
 例题1
例题1由于都为"≤"型,所以在三个约束式分别加上三个剩余变数x3、x4、x5,将不等式转化为等式。
第二步:列出初始单纯形表。
下图为一张完整的单纯形表,不同的教材画法有所差异,例如可以省略对b值和θ的部分单独进行列式计算。这里用最为全面的画法进行讲解。其中红色部分为约束条件原本的常数值,最后一行为检验数。中间的数值为各个变数的原始数值,其中基变数的係数,即蓝色数值(3×3)恰好构成一个单位矩阵,其检验数也恰好都为0。
 例一步骤1
例一步骤1第三步:更换基变数
最后一行中x1、x2检验数为不为负数或零,因此尚未取得最优值。需要去找另一个基本可行解,即将非基变数换入基变数中。如此循环下去,直到找到最优解为止。
通过基变数换入换出的操作需要有两个原则。第一,如果有多个检验数为正,那幺从最大的一个开始调整,因为变动检验数大的变数对于z值的变化越大,这道题目中x2的这一列的检验数最大,因此选择x2入基变数。但是为了保证係数的非负,b值与係数的比值θ即最右边的一行,应该选择数值最小的一个,因此这里选择4(<5),因此x4为出基变数。由3(最大检验数σj)和3(最小比值θ)确定的数值4称为主元,进行变换的方法称为高斯消元法,即用行的初等变换进行列消元。
 例一步骤2
例一步骤2第四步:继续叠代。
消元后x1、x3、x5变成基变数,同时係数和b值也发生了相应的变化,计算出检验数。发现x2的检验数仍为正数,将x2作为入基变数。通过θ最小法则,确定x5为出基变数。继续画出消元后的单纯形表。
 例一步骤3
例一步骤3第五步:确定所有检验数σj≤0,计算最优值Z*。
 例一步骤4
例一步骤4算法效率
在採用Bland's法则选择用于转轴操作的d和e(相同值的情况下取字典序最小)之后,可以证明单纯形法一定能够在有限步之后终止,但是最坏情况算法的时间複杂度为指数级别的,而且可以构造出让单纯形法的时间複杂度达到指数级别的具体实例。不过实践证明在绝大多数情况下单纯形法的效率非常令人满意。
单纯形法的最坏时间複杂度为指数级别,并不意味着线性规划不存在多项式级别的算法。椭球算法和内点算法均为解决线性规划的多项式时间算法。
定理意义
如今线性规划的理论与算法均非常成熟,在实际问题和生产生活中的套用非常广泛;线性规划问题的诞生标誌着一个新的套用数学分支———数学规划时代的到来。过去的 60 年中,数学规划已经成为一门成熟的学科。其理论与方法被套用到经济、 金融、 军事等各个领域。数学规划领域内,其他重要分支的很多问题是线上性规划理论与算法的基础上建立起来的, 同时也是利用线性规划的理论来解决和处理的。由此可见, 线性规划问题在整个数学规划和套用数学领域中占有重要地位。因此, 研究单纯形法的产生与发展对于认识整个数学规划的发展有重大意义。